Introduction

One of the most vexing concerns of reef aquarists is the problem of water chemistry. These concerns are founded in the knowledge that reef aquaria are really very tiny analogues of natural systems, and because of their small size chemical changes could occur that could adversely impact their livestock. The composition of natural sea water (NSW) is taken as the basis for measuring all changes in the water in aquaria, even though the standard for such natural seawater has historically been from the North Sea and not coral reefs. Chemical concentrations of most materials in seawater are presumed by most aquarists to be "conservative" and unchangeable, consequently, it is presumed that any changes away from the NSW concentrations are detrimental. On the gross scale of the world ocean's such a supposition has some validity, however in the close environment of the reef significant changes in many chemical constituents can and do occur. However, the data detailing with changes in coral reef water chemistry are sparse, and difficult to relate to the standard reef aquarium. Most aquarists, probably correctly, feel that they can't go wrong if they pursue a course of aquarium water chemistry management based trying to maintain "natural levels."

Implicit in such a management plan, although seldom directly stated, is the feeling that organisms somehow "use up," "change," or "consume" many of these chemicals, and in doing so, forever remove the chemicals from that reef aquarium system. This assumption is not completely false, some chemicals are "used up" and removed from the system, but most are not. Organisms are dynamic entities, and while some chemicals are temporarily sequestered away, such chemicals generally remain available in the system due to metabolic turnover. The only real exceptions to this as far as organisms are concerned are those chemicals, such as calcium, which get incorporated into an insoluble matrix. Once the chemical is removed from solution, even if that matrix, such as a coral skeleton or clam shell, remains in the aquarium, it is beyond the use of most organisms.

Another more important variable of these systems is chemical export via some sort of filtration or organism removal. The various types of filtration are widely regarded as very efficient, not at all efficient, or useless, depending on the authority consulted and presumably the whim of the moment. Unfortunately, there are few hard data to support any of the suppositions about export, except that it occurs. I hope to address the question of export methodologies and their effectiveness in a future research project, but for the present, we simply don’t have a good handle on what, or how, various chemicals leave our aquaria.

If we just started with sea water and had to deal with its changes over time, that would make the determination of what is happening in our systems relatively easy. Note that I didn't say, "Easy" but "relatively easy." However, we don't generally start with real seawater. Relatively few aquarists have access to natural seawater, and must use dried artificial mixes and some type of water to make the medium they put into their aquaria. These mixtures may vary significantly in many regards from natural water (See Atkinson and Bingman, 1999: AFM-online). Additionally, and importantly, we continually further alter the chemical constituents of our systems by adding food, and various other additives. The food is added based on our observations and knowledge of the organisms' needs. The other additives are added based on chemical tests, belief in the advertisements of the additive producers, barometric pressure, a toss of the dice, or maybe, just maybe, some rational guesstimate of depletion rates.

This report is the first of several, at least three and maybe more, examining the chemical constituents of marine aquarium water. It is a follow-up to my "Food and Additive Study" done about two years ago. In that project, I examined the chemical constituency of 15 popular foods and additives used by aquarists. The data from that study are available here: AFM-online. Using those data, we can reasonably well determine what chemicals may enter our systems. However, until now, we really didn't have any really good idea of what exactly is in our systems.

This study is an attempt to describe the chemical constituents of an "Average Reef Tank." The goal was to survey as wide a database as possible in the hope that the results of the study would be representative of reef tanks, in general. To that end, I advertised for volunteers willing to pay for the analysis of their tank water. I had hoped to get at least 15 volunteers, I got 18, and we were able to analyze the data from 23 different systems as well as one sample of artificial sea water. The participants had to answer a somewhat detailed questionnaire about their systems, and how those systems were maintained. Those responses and further analyses will constitute the basis for the forthcoming articles. This article will deal with the basic results of the water analyses of these systems.

Materials and Methods

I am an invertebrate zoologist, not an analytical chemist, so I couldn't do the necessary tests. They were done by a commercial analytical laboratory in the Seattle region.

The laboratory was:

AM TEST LABORATORIES, INC.
14603 NE 87th Street
Redmond, WA 98052.

They used two basic sources for analytical techniques:

EPA = Methods for Chemical Analysis of Water and Wastes, 1983 (available from National Technical Information Service, 5285 Port Royal Road, Springfield, VA 22161, Stock No. NTIS PB84-128677);

SM = American Public Health Association. 1992. Standard Methods for the examination of water and wastewater, 18th ed. American Public Health Association, Washington, D.C.

The concentrations were determined by Inductively Coupled Plasma Emission Spectrometry or ICP Scan, EPA method 200.7.

After verification of the participants, the laboratory was contacted and they sent sampling materials to me, these were plastic bottles labeled for each of three necessary samples from each aquarium. In total, each sample consisted of three 500 ml samples of aquarium water, one each for the metals, nitrogen chemistry, and conventional nutrients. After I received the sampling bottles, I prepackaged them and distributed them to the participants along with a questionnaire and instructions. The samples were returned me and then sent to the analytical laboratory. After the analysis, the data were returned to me, and electronically coded for analysis.

There were 24 samples analyzed: 23 aquarium samples, and one sample, of Instant Ocean(tm) (IO), prepared with 0 total dissolved solids RO/DI, mixed to 35 ppt, and stored for two weeks prior to testing in an FDA food-grade container. For comparative analyses, the chemical constituents for NSW were obtained from Weast, 1966.

The samples constituted independent samples without replication. The lack of replication significantly reduces the options for statistical analyses, however, it was necessary to obtain as wide a sample as possible. Given the cost of the sample analysis, analysis of replicates was simply too expensive. The lack of sample replicates precluded the use of tests such as analyses of variance (ANOVA), and other tests on means and variances.

However, basic descriptive techniques were possible as were many sample-to-sample comparisons. These analyses were dependent on the numerical values of the concentrations of the various constituents. The numerical values ranged from values as small as 0.0001 µg/l to as high as 12000 µg/l. This is a range variation in abundance of 100,000,000 times. Obviously, in any comparison those samples with high numerical values of any chemical could overwhelm the information in those with smaller amounts of chemicals. Consequently, all tests were run twice, once using untransformed data, and the second time with a log normal transformation of the data. A log normal transformation of the data involves taking the value for the datum, adding one to it, and taking the natural logarithm of the sample. Algebraically, this transformation is indicated by the following terminology: ln(x+1), where x = the sample datum. Such a log-normal transformation is commonly done in those analyses where data may very over several orders of magnitude and it reduces the influence of large values and increases the influence of smaller values. The transformation has known properties and quite useful in comparisons involving widely dissimilar data values. In these samples, this transformation reduced the influence of relatively highly concentrated materials, for example Sodium, Sulfur, and Magnesium.

In the initial analyses, the salinity varied widely. I presumed many of the constituent abundances were correlated with salinity; for example, if two batches artificial salt mix was made up, one a concentration of 30 ppt, and the other to a concentration 36 ppt, there would be differences in all of the materials found in the two samples. However, none of these differences would be due to any "in tank" changes or variables. Consequently I normalized all data by adjusting all the samples to the same sodium concentration as found in the tabled value for NSW; this was done by multiplying all concentrations by a constant consisting of the sodium concentration divided by the sodium concentration in NSW. Finally, after the initial analyses were completed, I removed from consideration all chemicals found in NSW but below detection limits in all of the samples.

The elements removed from these analyses were: Beryllium, Cadmium, Chromium, Iron, Lead, Manganese, Mercury, Selenium, Silver and Yttrium.

Descriptive statistics were determined on a spreadsheet, Quattro Pro (Corel, 1997). The relationships between and within the samples were investigated using a series of analytical programs called the Community Analyses System, V. 5.0 (Bloom, 1994). Initially, the samples underwent a process called classification. The index used to classify the samples was the Percent Similarity (or Bray-Curtis) Index.

Bray-Curtis Index

This index compares the relative proportion of each element in each sample by subtracting one from the other. The values for all the elements are summed and subtracted from one. Two samples are considered to be identical if they have a proportional similarity of 1 and completely dissimilar with a value of 0. During the process of "classification," each sample was compared with all other samples and all possible groups of samples. Finally a representation of which samples are most similar to each other is determined. The samples then are arranged in series of groups based on relative similarity. The graphical representations of such relative similarity lineages resulting from these analyses are called dendrograms (see Figures 1-4). Such dendrograms typically show clusters of samples, and hence the whole process of classification is sometimes called "cluster analysis." Such an analysis results in an unambiguous, quantitative and replicable way of showing sample similarity.

Subsequent to the classification were examined by ordination. Ordination is a statistical approach and methodology used to suggest interrelationships between samples. There are a number of different techniques to do this, I used the process called Principal Coordinate Analysis as it has fewer inherent biases than many of the other processes, provided the data are appropriate and the process is done correctly.

In our natural three-dimensional world, objects may be described and compared based on the three principal dimensional axes of length, width, and height. Ordination results in a similar comparison, but in an artificial universe with more than three dimensions. In the case of this study, ordination may be thought of as a process of creating a mathematically defined universe and arraying the samples in it based on their relative chemical concentrations. This universe would not have just the normal three spatial dimensions. Instead, it would have a number of dimensions corresponding to the total number of chemicals or constituents being tested. The data from the samples are placed in the volume created in this universe and manipulated to "explain" most of the differences between them by creating and rotating the dimensional axes to maximize the differences on the first axis, while minimizing those differences on all subsequent ones. Ideally, one tries construct these axes so that most of the information is contained on the first three axes.

Most people, including me, have significant trouble visualizing a fourth, fifth, sixth or seventh dimensional volume (or in the case of this study, a 30 to 40 dimensional volume). Three dimensions work just fine, for visualizations, IF we can get there in the analyses. In diverse data sets such as these, often the sample variability is so high that one really does need to think about the samples in five or more dimensions. In these cases, we are generally out of luck as far as visualizing the samples, and have to deal with paper data. For these ordination analyses, the data were classified using Gower's Distance Index, and the concentrations were zero mean and unit variance transformed.

Gower's Distance Index

Subsequent to Ordination, the centroid of the data in the volume determined by first three primary axes in ordination space was calculated and a non-parametric (Mann-Whitney) 95% Confidence Interval Interval was calculated about that centroid (See Bloom, 1994, for this procedure and for a good description of classification and ordination techniques).

To help interpret the data, particularly the classification and ordination the sample ranks for each constituent were calculated. The top three and the bottom three ranks were generally determined.

Results

A summary of the concentration data is given in Table 1. Although some chemicals, particularly Calcium and Sodium, are generally found in values that approximate those of natural seawater, the data are more notable for the diversity of values than for their consistency. Many of the rarer trace elements, such as Beryllium and Selenium, if present, were below detectable levels. Generally, toxic materials such as Cadmium, Lead and Mercury were also undetectable.

In contrast, the values for other materials, notably Antimony, Cobalt, and Titanium were hundreds of times more concentrated in the average sample than in natural seawater.

In the examination of similarity differences calculated with the methods used here, it is often useful to be able to compare the ranking of various chemicals across the samples. In other words, "Were there samples that contained consistently high values of many chemicals (or showed high rankings for those chemicals)? " Similarly, "Were there samples that were always low?" The rankings are shown in Table 2, and several samples are evident for their differences.

As might be expected from independent samples, the data are clearly scattered. For example, sample CC is full of extremes; it has high values of Calcium, Cobalt, Copper, Potassium, Nickel and Phosphorus and low values of Aluminum, Antimony, Arsenic, Boron, Barium, Lithium and several other chemicals. Sample S1, on the other hand is has 12 high ranks and only 1 low rank, while Sample AH is almost the reverse with 10 low ranks and 1 high rank. As might be expected there are also a lot of values in between. In subsequent articles, I will investigate some of causes and concerns of this disparity in samples.

Dendrograms

I would imagine the first thing the average reef aquarist would say when looking at the figures below is, "Yikes." (Actually, I am being "polite," I think the first thing said would be considerably more "earthy and heartfelt.")

Don't despair, these figures are actually very simple to understand. A dendrogram is a figure that branches like a tree ("dendron" means "tree"). In these figures, the trunk is coming from the left and the branches show relationships, based on chemical abundances. What they show are the relationships of the samples indicated at the left. Each branch typically separates two groups of samples on the basis of shared characters. Each group has more in common with other members of its group (and sometimes the group is only the one sample) than all other samples. So in the first example below, the first branch point from the right is at a similarity of about 0.86 or 86 percent. That branching splits off sample RC2 from all the others. All the other samples are more similar to themselves than to RC2. The second branch occurs at a similarity of about 0.92, and splits the remaining 24 samples into two groups. The smaller group, consisting of samples EB, DL, GD, S1, DC, and SC is separated from all other samples. From Table 2, it is evident that these samples have little overall in common except that they generally have several extreme ranks of various chemicals. The larger group is further subdivided into two other groups of samples each more similar amongst themselves than to others. Any of the samples in the two shades of blue are more similar to each other than any of them are to those samples in green or orange. From examining these data, one can see that the samples in blue are more similar to either artificial sea water or natural sea than are the samples in green or orange. In the discussion session that follows, I will discuss some of the reasons for these groupings.

Notice the changes when all of the data are log normally transformed in Figure 2. Here the effects of very high concentrations are reduced, and the effects of very small concentrations of chemicals are enhanced. Natural Sea Water, with a lot of elements in trace amounts becomes very distinct. All of the other samples are more than 90 % similar, and even though they are grouped, these groups are fairly similar amongst themselves. The large group indicated in gray containing IO is comprised of many samples that were initially formed from IO water.

Figure 3 shows the relationships of the samples when the effects of trace elements present in natural sea water, but below the detection limits in all the samples, are removed from the analysis. Most of these samples are actually quite similar to each other and to NSW and IO. Only a few samples are somewhat oddballs. Interestingly, these are some of the same dissimilar samples shown in the upper branches of the dendrogram in Figure 1.

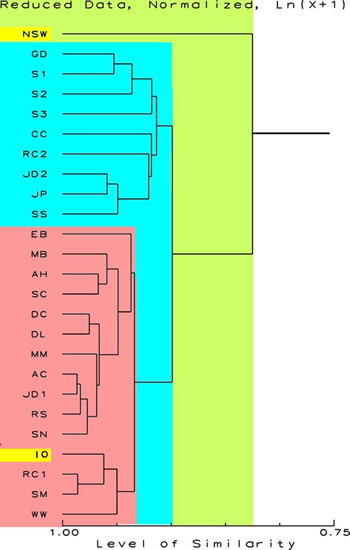
In Figure 4, the data used in the analysis are log normally transformed, and as a result, NSW is again separated from all other samples. This is undoubtedly due to the abundance of elements present in trace amounts. Such materials really don’t exist in the aquarium samples; the samples either have materials in relatively great amounts, or they lack them all together. All of the remaining samples are at least 90% similar, and include IO. No matter what has been done to these aquaria, the water in them is still very similar across all the samples.

Figure 1. Proportional Similarity Index Dendrogram showing the relative similarity of the sample. The scale at the bottom is in percent similarity. All data are included and no transformations have been done. The data for NSW and IO are highlighted.

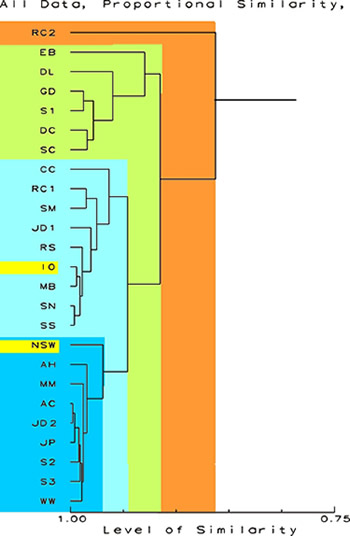
Figure 2. Proportional Similarity Index Dendrogram showing the relative similarity of the sample. The scale at the bottom is in percent similarity. All data are included and the ln (x+1) transformations have been done. This emphasizes the contribution of rarer chemicals. The data for NSW and IO are highlighted.

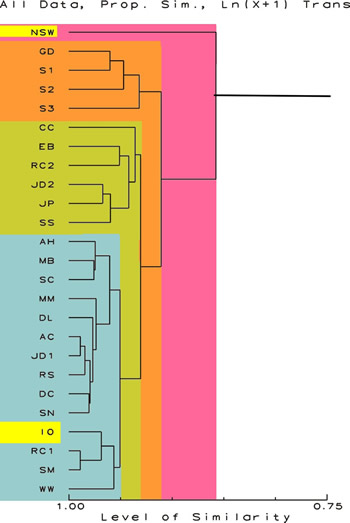
Figure 3. Proportional Similarity Index Dendrogram showing the relative similarity of the sample. The scale at the bottom is in percent similarity. This figure shows the relationships with the values for sodium and undetectable elements removed. No ln (x+1) transformations have been done. This de-emphasizes the contribution of rarer chemicals and sodium in the NSW data. The data for NSW and IO are highlighted.

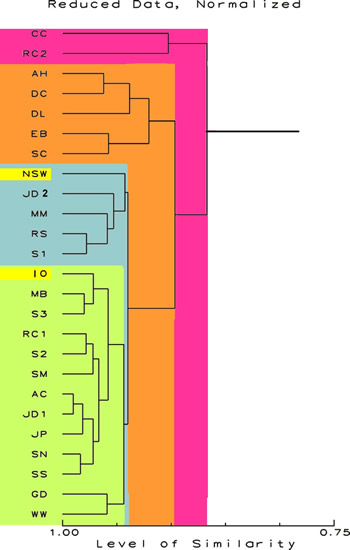
Figure 4. Proportional Similarity Index Dendrogram showing the relative similarity of the sample. The scale at the bottom is in percent similarity. This figure shows the relationships with the values for sodium and undetectable elements removed, and the ln (x+1) transformations have been done. This further de-emphasizes the contribution of rarer chemicals and sodium in the NSW data. The data for NSW and IO are highlighted.

The numerical results of the efficiency of the ordination at grouping the data in similar groups (or in the language of the test "explaining the variation") are indicated in Table 3. It can be seen that manipulations along the first 3 dimensions (or vectors) explain over 96 percent of the variation. This is really a quite good result. Normally, one considers that an ordination result is good if this value is 75 percent or better. This means we can use the data derived from the ordinations, with some degree of confidence.

The following illustrations, Figures 5-7, are perhaps the most important figures in the article. They show the result of the ordination analyses in a three-dimensional space with each axis corresponding to the dimensions indicated above; each figure shows the plot of the data from a different direction. The positions for the centroid of the sample grouping, IO and NSW are indicated. The rectangle in the center each figure is the representation of the 95% Confidence Interval Limits around the centroid. That means that one can say that any sample outside of the boundary of that line is statistically significantly different from centroid of the group, with a 95% chance that that statement is correct. Or phrased another way, all of the samples shown as being outside the line in any one of the views have only one chance in twenty - or less - of being similar to the samples inside the limits.

This technique and the dendrograms do show that there are some defined groups of samples that have within themselves similar samples. There are also a large number of samples, including specifically both NSW and IO, that have chemical constituent arrays that are statistically significantly different from the majority of the samples.

The take home message from these results is that there are some discrete groups of samples, but that at least a third of the samples are from aquaria that vary in some significant way not only from each other, but from both natural sea water, and artificial sea water made from one of the most popular of artificial sea water mixes.

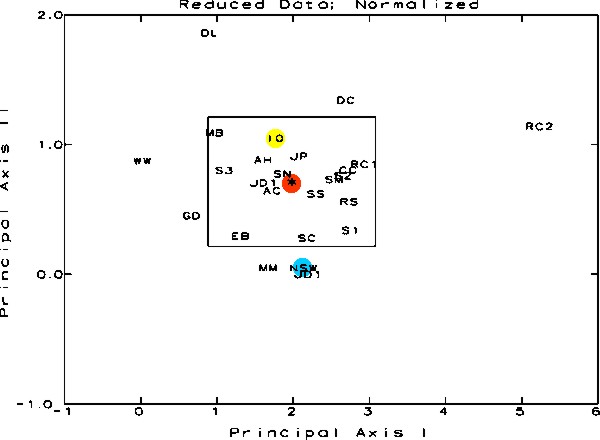
Figure 5. This figure is a result of the Principal Coordinate and Recovery Analysis. The samples are represented by their letter designations and should be visualized in 3-Dimensional space. The three axes for this space are Principal Axes I, II, and III, each oriented perpendicular to one other. This figure shows the data in relation to Principal Axes I and II. The rectangle is the 95% Confidence Interval around the centroid of the distribution. Any sample shown outside the limits in any one graph is statistically significantly different from the average of all of the samples. The position of the cluster centroid is shown in red, NSW in blue and IO in yellow.

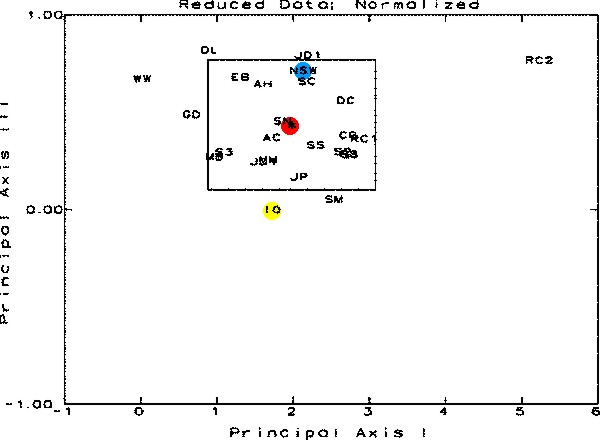
Figure 6. This figure is a result of the Principal Coordinate and Recovery Analysis. The samples are represented by their letter designations and should be visualized in 3-Dimensional space. The three axes for this space are Principal Axes I, II, and III, each oriented perpendicular to one other. This figure shows the data in relation to Principal Axes I and III. The rectangle is the 95% Confidence Interval around the centroid of the distribution. Any sample shown outside the limits in any one graph is statistically significantly different from the average of all of the samples. The position of the cluster centroid is shown in red, NSW in blue and IO in yellow.

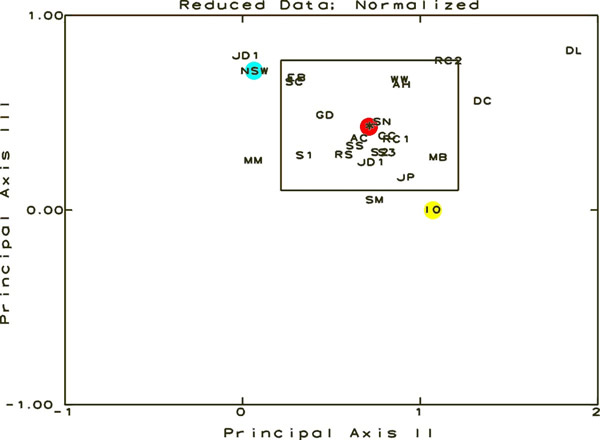
Figure 7. This figure is a result of the Principal Coordinate and Recovery Analysis. The samples are represented by their letter designations and should be visualized in 3-Dimensional space. The three axes for this space are Principal Axes I, II, and III, each oriented perpendicular to one other. This figure shows the data in relation to Principal Axes II and III. The rectangle is the 95% Confidence Interval around the centroid of the distribution. Any sample shown outside the limits in any one graph is statistically significantly different from the average of all of the samples. The position of the cluster centroid is shown in red, NSW in blue and IO in yellow.

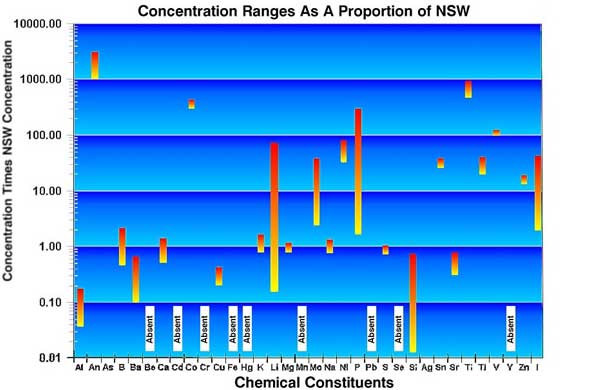
Figure 8. This figure is a graphical representation of the data in Table 3. Note that the concentration ranges are given on a logarithmic scale. Values near 1.00 are similar to NSW, those greater or lesser are proportionally different from NSW.

Discussion and Conclusions

Many hobbyists are fond of saying that there is no "one" correct way to set up a reef tank, that instead of "One True Path Toward Righteousness and Light," there are an almost infinite number of ways to set up a reef tank. Well, even the most adventurous of these folks would likely not have guessed the differences found in these 23 reef tanks, some with problems (more about that in subsequent articles), but even so, all are supporting a broad and diverse array of animals.

In most cases, it appears that about the only similarities that Reef Aquarium Water has to Natural Sea Water is that they both are wet, and they both contain somewhere in the range of three and one half percent (or 35%) salt by weight. It can truly be said that very little else is similar. The proportional data given in Table 4 and Figure 8 show that while some of the constituents in these tanks are near the proportions found in sea water, some others are absent, for example Beryllium; a few are present in very reduced proportions, for example Aluminum; and others are present in significantly higher proportions, such as Antimony, Titanium, and Iodide. While many of the chemicals are found in similar amounts in all the tanks, others vary widely. Lithium, for example, varies between the largest and smallest concentrations by almost a factor of 500 times.

Nevertheless, the tank waters surveyed in this study are apparently relatively similar in many regards. The dendrograms generally show that while there are a group of "outlier" samples, most of the samples are clustered in one to four groups all similar to each other with about Proportional Similarities from about 85 percent to 90 percent. This similarity is likely due to the widespread usage of Instant Ocean™ as the salt mix used by the aquarists in the study. However, interestingly enough, many of these same tanks are in different similarity clusters from that containing Instant Ocean™.

Even though many of the systems start at the same point, and have some overall similarities, the cumulative results of the factor-by-factor differences, indicate that the overall sample group is statistically significantly different from both IO and NSW. This is indicated in Figures 5-7, where it is evident that the artificial and natural sea waters have distributions that are statistically significantly different from the average point (the sample "centroid") describing all the samples.

Most aquarists aspire to the goal of maintaining the liquid medium in their aquarium as similar to NSW as is possible. Yet, they try to do this without any way to test most chemicals, and without an understanding of the dynamic nature of the concentration of those chemicals in semi-closed systems such as these aquaria. A significant reason for this problem is that the basic water obtained when artificial salt mixes (see Atkinson and Bingman, 1999 and the IO data in this study) are prepared bears very little similarity to NSW, but even aquarists using NSW as the initial medium don't have tanks where the chemical composition bears much similarity to Natural Sea Water. Sample GD was from a tank that uses NSW as a medium, and as shown in the dendrograms, no matter how the data are manipulated, that particular sample is never very similar to NSW.

Questions as to why these differences occur, and discussions of their importance will be the subject of the subsequent articles discussing the results of this project. For the present, it is apparent that much of the worry over various chemical compositions and levels is simply unnecessary. It appears that the animals have significant latitude in altering either their external or internal environments to adjust for the differences seen in this study.

References Cited:

Atkinson, M. and Bingman, C. 1999. The Composition of Several Synthetic Seawater Mixes.. March 1999 Aquarium Frontiers On-line.

Bloom, S. A. 1994. The Community Analyses System, V 5.0. Ecological Data Consultants, Inc., Archer, Florida.

Corel Corporation. 1997. Quattro Pro, V. 8. 0. 0. 709. Copyright (c) 1997 Corel Corporation and Corel Corporation Limited. All rights reserved.

Weast, R. C. 1966. Ed. The Handbook of Chemistry and Physics. 46th edition. Chemical Rubber Company. Cleveland, Ohio. Page F-110.

Acknowledgments:

The following people participated in the study by providing one or more water samples and much of the cost of the analyses for those samples, or by providing cash donations to help fund the study. Three people made cash contributions, which largely covered the costs of the analysis not covered by the participants, as well as covering all the other costs of the study. I would like to especially thank one donor, damnhippo at reefs.org, whose generous contribution of a very large grant covering over half the costs of the project not only met all the remaining costs of the study, but also provided for assistance to the next project, on exports.

I thank Mark Boenisch, Eric Borneman, Cliff Carter, David Celentano, Allen Chantelois, Steven Collins, Gregory Dawson, John Delery, Adrian Harris, Deborah Lang, John Link, Matthew Mengerink, Steven Miller, Steven Nichols, Jaroslaw Pillardy, Robert Schnell, Sandra Shoup, William Wiley, the staff at Reef Central and anonymous contributors for contributing water samples. I also thank Matthew Hennek, Matthew Davis, and Win Phinyawatana for providing cash donations to support this venture. Without all of your assistance, this project would not have been possible.